什么是多项式回归 多项式回归和多元线性回归的区别
时间:2025-04-23 来源:互联网 标签: PHP教程
在数据科学和统计分析的领域中,回归分析是一种重要的方法,它用于理解变量之间的关系。在众多回归模型中,多项式回归和多元线性回归是两种常见的技术。本文将详细介绍这两种回归分析的方法,探讨它们的区别以及适用场景。
一、什么是多项式回归?
多项式回归是一种回归分析方法,它通过引入自变量的幂次项来拟合数据,使得模型可以捕捉到非线性关系。具体来说,假设有一个一元多项式回归模型,其形式为:
\[y=\beta_0+\beta_1x+\beta_2x^2+\cdots+\beta_nx^n+\epsilon\]
其中,\(y\)是因变量,\(x\)是自变量,\(\beta_i\)是待估计的参数,\(n\)是多项式的阶数,\(\epsilon\)是误差项。这种模型能够适应各种复杂的非线性关系。
1)优点:
灵活性强:可以拟合复杂的非线性关系。
简单易用:只需引入高阶项即可扩展模型。
解释性强:可以通过模型系数理解自变量对因变量的影响程度。
过拟合风险:如果阶数过高,可能会导致过拟合,即模型在训练数据上表现良好,但在新数据上表现不佳。
计算复杂度增加:阶数越高,计算量越大。
易于理解:模型简单直观,易于解释。
计算效率高:计算过程相对简单,适合大规模数据处理。
广泛应用:适用于大多数线性关系的建模需求。
线性限制:假设因变量与自变量之间是线性关系,这在某些实际情况下可能不成立。
多重共线性问题:如果自变量之间高度相关,可能导致模型不稳定。
模型形式与复杂度:
数据适应性:
应用场景:
计算复杂度与资源消耗:
2)缺点:
二、什么是多元线性回归?
多元线性回归则是处理多个自变量的线性回归模型,其一般形式为:
\[y=\beta_0+\beta_1x_1+\beta_2x_2+\cdots+\beta_px_p+\epsilon\]
在这个模型中,\(y\)是因变量,而\(x_1,x_2,\ldots,x_p\)是多个自变量,\(\beta_i\)是待估计的参数,\(p\)是自变量的个数,\(\epsilon\)是误差项。这个模型假定因变量与自变量之间存在线性关系。
1)优点:
2)缺点:
三、多项式回归和多元线性回归的区别
多项式回归:适用于非线性数据,通过引入高阶项来增强模型的表达能力。模型较为复杂,容易发生过拟合。
多元线性回归:适用于多变量之间的线性关系。模型简单,易于理解和计算。
多项式回归:能够更好地适应非线性数据,但需要谨慎选择多项式的阶数以避免过拟合。
多元线性回归:主要适用于自变量与因变量之间存在线性关系的场合。如果关系是非线性的,则可能效果不佳。
多项式回归:常用于需要捕捉复杂非线性关系的领域,如物理学、工程学中的曲线拟合问题。
多元线性回归:广泛应用于经济学、社会科学等领域中的预测和分析任务,例如房价预测、市场分析等。
多项式回归:随着阶数的增加,计算量显著增加,对计算资源的要求较高。
多元线性回归:计算相对简单,资源消耗较少,适合处理大规模数据集。

在选择使用多项式回归或多元线性回归时,需要根据具体的问题和数据特征来决定。如果数据呈现明显的非线性关系,且对模型复杂度有较高的容忍度,那么多项式回归可能是更好的选择。反之,如果数据基本符合线性关系且需要高效、简单的模型,那么多元线性回归更为合适。无论采用哪种方法,都需要仔细评估模型的表现,避免过拟合或欠拟合,确保模型的稳健性与可靠性。
以上就是php小编整理的全部内容,希望对您有所帮助,更多相关资料请查看php教程栏目。
-
 毛利无能是什么梗?揭秘毛利小五郎爆笑名场面,网友玩梗停不下来! 2026-01-19
毛利无能是什么梗?揭秘毛利小五郎爆笑名场面,网友玩梗停不下来! 2026-01-19 -
 《三国:谋定天下》游戏攻略大全 2026-01-19
《三国:谋定天下》游戏攻略大全 2026-01-19 -
 蚂蚁庄园小课堂2026年1月16日最新题目答案 2026-01-19
蚂蚁庄园小课堂2026年1月16日最新题目答案 2026-01-19 -
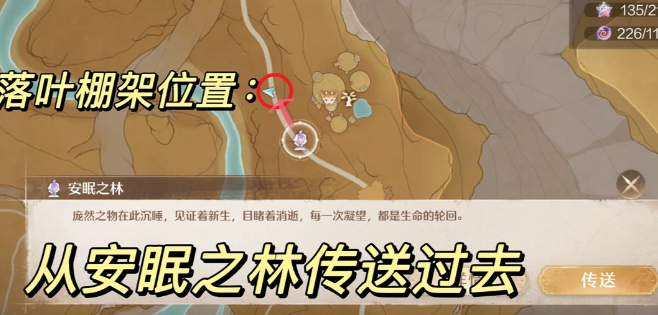 无限暖暖2.1林间欢动时光落叶棚架位置指引 2026-01-19
无限暖暖2.1林间欢动时光落叶棚架位置指引 2026-01-19 -
 龙族卡塞尔之门七宗罪选择推荐 2026-01-19
龙族卡塞尔之门七宗罪选择推荐 2026-01-19 -
 神界原罪2暴君套装位置介绍 2026-01-19
神界原罪2暴君套装位置介绍 2026-01-19





