平衡二叉树的实现原理和常见操作方法
时间:2024-12-07 来源:互联网 标签: PHP教程
在数据结构和算法的学习中,平衡二叉树是一个非常重要的概念。它不仅在实际应用中有广泛的使用,也是理解更复杂数据结构的基础。今天,我们就来深入了解一下平衡二叉树的实现原理和常见操作方法。
一、什么是平衡二叉树?
我们需要明确什么是平衡二叉树。简单来说,平衡二叉树是一种特殊类型的二叉树,其中每个节点的两个子树的高度差最多为1。这种特性使得平衡二叉树的高度保持在对数级别,从而保证了查找、插入和删除等操作的时间复杂度都是O(logn),大大提高了效率。
二、平衡二叉树实现原理
节点旋转
平衡二叉树的核心在于保持平衡,而保持平衡的关键手段是节点的旋转操作。旋转分为左旋和右旋,它们可以调整树的结构,确保任何节点的两个子树高度差不大。
左旋:以某个节点作为支点,将其右子节点或右子节点的左子节点变为自己的根节点。
右旋:与左旋相反,将左子节点或左子节点的右子节点提升为根节点。
平衡因子
除了旋转,我们还需要一个衡量标准来判断何时进行旋转——这就是平衡因子的概念。平衡因子定义为节点的左子树高度减去右子树高度。根据这个值的正负和大小,我们可以决定执行哪种旋转以及旋转的方向。

三、常见操作方法
搜索操作
搜索操作在平衡二叉树中与普通二叉搜索树类似,都是基于比较节点值来决定向左还是向右递归搜索。由于树是平衡的,所以最坏情况下的时间复杂度是对数级别的。
插入操作
插入新节点时,我们首先按照普通二叉搜索树的规则插入,然后更新父节点和祖父节点的平衡因子。如果发现某个节点的平衡因子超出范围(通常设为[-1,1]),则通过旋转操作调整树的结构以恢复平衡。
删除操作
删除节点比插入稍微复杂一些,因为它可能涉及到更多的旋转操作来恢复平衡。删除节点后,需要检查被删除节点的父节点是否失衡。如果是,就通过一系列旋转来调整。这个过程可能涉及到多种旋转组合,比如先左旋再右旋或者反之。
高度计算
平衡二叉树的高度计算采用递归的方式,从根节点开始,依次计算每个节点的高度,最后返回树的高度。
平衡二叉树通过精妙的设计保证了高效的数据访问和更新速度,是许多高级数据结构(如红黑树、AVL树)的基础。掌握其实现原理和操作方法是深入理解数据结构的起点。虽然实际操作中可能需要处理复杂的旋转和维护平衡因子的逻辑,但正是这些细节体现了数据结构设计的智慧和计算机科学的美妙。
以上就是php小编整理的全部内容,希望对您有所帮助,更多相关资料请查看php教程栏目。
-
 怪物猎人(踏上龙神之路,探寻天空的宝藏) 2026-01-13
怪物猎人(踏上龙神之路,探寻天空的宝藏) 2026-01-13 -
 燕云十六声无名剑法好还是积矩九剑好 2026-01-13
燕云十六声无名剑法好还是积矩九剑好 2026-01-13 -
 预视武宗飞叶派怎么玩 2026-01-13
预视武宗飞叶派怎么玩 2026-01-13 -
 噬血代码2配置要求 2026-01-13
噬血代码2配置要求 2026-01-13 -
 燕云十六声云蛇王骨在哪里 2026-01-13
燕云十六声云蛇王骨在哪里 2026-01-13 -
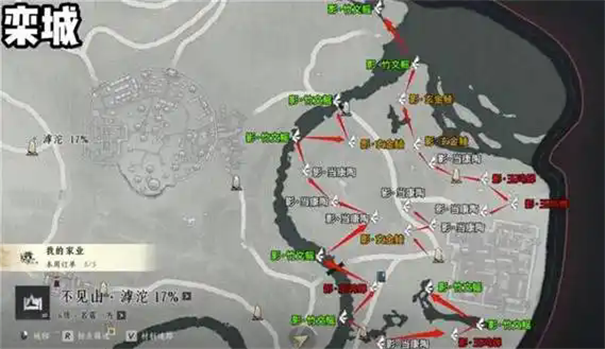 燕云十六声不见山滹沱过河玩法攻略 2026-01-13
燕云十六声不见山滹沱过河玩法攻略 2026-01-13





