详解PHP怎么使用动态规划实现最优红包组合

今天PHP爱好者为您带来最近在做一个小需求，每笔订单会根据金额决定用户可以使用的红包最大值，如果用户选择使用红包，需要帮助用户从拥有的红包列表里选取最优的红包组合，要求组合出的红包值最接近或等于可以使用的红包最大值。希望对大家有所帮助。

最近在做一个小需求，每笔订单会根据金额决定用户可以使用的红包最大值，如果用户选择使用红包，需要帮助用户从拥有的红包列表里选取最优的红包组合，要求组合出的红包值最接近或等于可以使用的红包最大值。后面思考了一圈，这不就是 『0-1背包问题』么，终于可以把以前学过的 『动态规划』 算法拿来实战一下了！

动态规划是什么

动态规划 (Dynamic programming 简写：DP)是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。

动态规划常常适用于有重叠子问题和最优子结构性质的问题，动态规划方法所耗时间往往远少于朴素解法。

动态规划适用场景

一般使用动态规划来解决求最优解的问题。在解决问题的过程中需要多次决策，而每次决策都有产生一组状态，然后从最优的决策中继续下一次的决策，最终找到最优的结果。

另外动态规划还具有3个特征，如下：

最优子结构性质

如果问题的最优解所包含的子问题的解也是最优的，我们就称该问题具有最优子结构性质（即满足最优化原理）。从而我们可以通过子问题的最优解，推导出问题的最优解，也可以理解为后面阶段的状态可以通过前面阶段的状态推导出来。

无后效性

即子问题的解一旦确定，就不再改变，不受在这之后、包含它的更大的问题的求解决策影响。

可以简单理解为 在推导后面阶段状态的时候，我们只需要关心它前一阶段的状态状态，不用去关心这个状态是怎么一步步推导出来的。第二个含义就是某个阶段的状态一旦确定下来，就不会受之后阶段的决策影响。

子问题重叠性质

子问题重叠性质是指在用递归算法自顶向下对问题进行求解时，每次产生的子问题并不总是新问题，有些子问题会被重复计算多次

0-1背包问题

上面的理论比较抽象，和扯犊子一样的，来看下经典的背包问题。

假设现在有5个物品他们的重量分别是 2, 2, 5, 11, 4, 现在有一个背包，能承受的最大重量是 10，请选择合适的物品放入背包，那么能组合出的物品最大重量是多少?

不同的物品组合会有多种不同的状态，我们可以使用 f(i, w) 来表示一种状态，其中 i = index 表示第几个物品， w = weight 表示当前的总重量。

整个问题的求解需要经过 『n』 个阶段，每个阶段都需要决策一个物品是否放入背包，决策的结果只有2种 『放入』 或者 『不放入』。在决策完一个物品后，背包中的物品重量会有很多种不同的状态，我们需要把每一层的 重复状态 合并，然后只留下不同的状态。然后基于上一层的状态结果来推导出下一层的状态结果。最终全部物品决策完就可以找到最优的组合解。

第0（其实也就是第一个物品，按照习惯从0开始下标吧）个物品的重量是2，然后开始决策是否放入背包，结果只有2种。如果放入背包那么此时背包的重量就是2，如果不放入背包那么背包的重量就是0.记作 $status[0][0] = true; 和 $status[0][2] = true; 和上面的 f(i, w) 一样，前一位表示物品，后一位表示重量。

第1个物品的重量还是2，然后开始对他决策，决策只有2种选择 放入背包 或者 不放入背包，但是它的状态组合却多了，因为它要基于之前的背包状态来判断当前的状态。对第1个物品完成决策后会有3个状态(其实是4个状态，不过有1个重复的就不算了 还是算3个不同的状态)。

如果决策当前物品放入背包,第0个物品不放入背包，此时的状态是 $status[1][2 + 0] = true; => $status[1][2] = true;
如果决策当前物品放入背包,第0个物品也放入背包，此时的状态是 $status[1][2 + 2] = true; => $status[1][4] = true;

如果决策当前物品不放入背包,第0个物品不放入背包，此时的状态是 $status[1][0 + 0] = true; => $status[1][0] = true;
如果决策当前物品不放入背包,而第0个物品放入背包，此时的状态是 $status[1][0 + 2] = true; => $status[1][2] = true;

其中 $status[1][2] 是重复的，所有会产生3种结果。

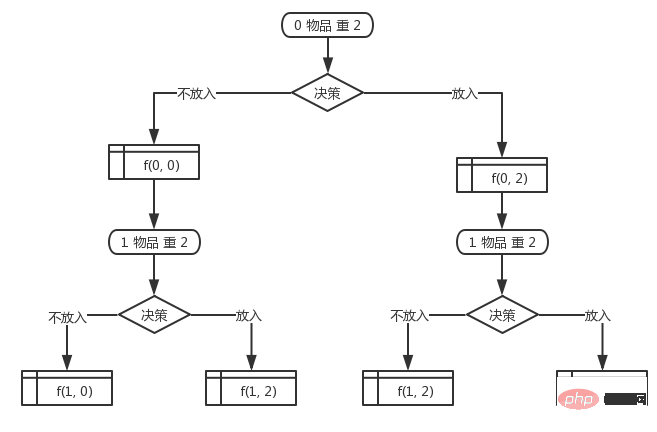
后面的物品也是以此类推，直到对所有的物品都决策完，整个状态的数组就都找出来了，然后只需要在最后一层找到一个值为true的最接近最大值(上面的例子中是10)的值就是背包能承受的最大值。然后可以从最后依次往前推就可以找出对应的物品下标，也就是哪些物品的组合是这个最优解组合了。

推导过程如下图：

实际上在上面的推导过程中就是动态规划的解题思路。把问题分解为多个阶段，每个阶段对应一种策略。然后记录下每个阶段的状态（注意要去掉重复项），然后通过当前状态的可能推导出下一个阶段的所有状态可能，动态的推导下去。

PHP实现伪代码：

function dynamicKnapsack($arr, $n, $max){
    // 初始化二维数组
    $status = [];
    for ($i = 0; $i < $n; $i++) {
        // max + 1 才能有max的值 因为下标从0开始的
        for ($j = 0; $j < $max + 1; $j++) {
            $status[$i][$j] = 0;
        }
    }
    // 第一个物品特殊处理
    // 对第一个物品决策不放入
    $status[0][0] = 1;
    // 对第一个物品决策放入
    if ($arr[0] <= $max) {
        $status[0][$arr[0]] = 1;
    }

    // 开始动态规划进行决策 -- 外层是物品
    for ($i = 1; $i < $n; $i++) {
        // 决策放入背包
        for ($j = 0; $j < $max + 1; $j++) {
            // 找到他上一层的组合，在上一层的基础上变更当前层的结果
            if ($status[$i - 1][$j] == 1) {
                $status[$i][$j + $arr[$i]] = 1;
            }
        }
        // 决策不放入背包
        for ($j = 0; $j < $max + 1; $j++) {
            // 找到上一层的组合直接取上一层的值
            if ($status[$i - 1][$j] == 1) {
                // $status[$i][$j] = 1; 等价于下面
                $status[$i][$j] = $status[$i - 1][$j];
            }
        }
    }
    // 寻找最优组合
    $best = [];
    $j = 0;
    // 为了找到寻找最优解的开始位置
    // 也就是当前能组合出的最大值是多少
    // 最后一行是最大的组合，它包含了所有都放入的结果
    // 最终确定了j开始的位置
    for ($j = $max; $j >= 0; $j--) {
        if ($status[$n - 1][$j] == true) {
            break;
        }
    }
    for ($i = $n - 1; $i >= 1; $i--) { // 外层遍历行
        if ($j - $arr[$i] >= 0 && $status[$i - 1][$j - $arr[$i]] == 1) {
            var_dump('buy this product: '.$arr[$i]);
            $best[] = $i;
            $j = $j - $arr[$i];
        }
    }
    if ($j != 0) {
        var_dump('buy first product:'.$arr[0]);
        $best[] = 0;
    }
    return $best;}// 测试数据$arr = [
    2, 2, 5, 11, 4,];$n = 5;$max = 10;$best = dynamicKnapsack($arr, $n, $max);var_dump($best);

如果求的结果是 11，得出的结果是 4, 5, 2 的组合，你可能会有疑问不是还有11这个结果么，刚好它一个就满足了不是么。我觉得这个应该是看实际的需求。比如我这次的需求是把红包按过期时间排序，快过期的优先使用，然后我在组装数据的时候按过期时间顺序强行把快过期的红包放到数组最后面拼成数组，那最后的4就是最接近快过期的红包了，我要优先消耗掉这个红包，如果使用了4那11就不能使用了，只能继续去前面找，就是这么回事！

总结

这段代码的时间复杂度是多少? 耗时最多的部分是中间的嵌套2层循环，所有时间复杂度是 O(n*max)，其中 n 表示物品的个数，max表示最大的承重。

空间复杂度是一开始申请的数组空间 O(n*max+1) 加上计算结果的累加有可能出现 O(n*2*max) 的情况，空间消耗还是很高的。

总体来说这是一种空间换时间的思路。另外在中间决策的嵌套循环里如果使用j从小到大遍历的话会出现for循环重复计算的问题。                                       

以上就是详解PHP怎么使用动态规划实现最优红包组合的详细内容，更多请关注php爱好者其它相关文章！